Home >> Advanced

>Motion

<< Previous

Next >>

Model

Internally, ALMotion keeps a model of NAO up to date each cycle. Much of this information is available to users via the following three methods:

          # Example showing how to get a simplified robot position in world.
          useSensors  = False
          result = proxy.getRobotPosition(useSensors)
          print "Robot Position", result

          # Example showing how to get the end of the right arm as a transform 
          # represented in torso space. The result is a 4 by 4 matrix composed
          # of a 3*3 rotation matrix and a column vector of positions.
          name  = 'RArm'
          space  = 0
          useSensorValues  = True
          result = proxy.getTransform(name, space, useSensorValues)

          # Example showing how to get the position of the top camera
          # The position is a representation containing
          # The x,y and z coordinates in meters
          # The wx, wy, wz euler angles in radians
          name  = 'CameraTop'
          space  = 1
          useSensorValues  = True
          result = proxy.getPosition(name, space, useSensorValues)
        

Denavit and Hartenberg method

The Denavit and Hartenberg method simplifies the description of serial manipulators. This method gives a rapid and precise method for computing the forward Kinematic model of the robot. Inside the Robot, the modified notation is used. We commonly name it mDH.

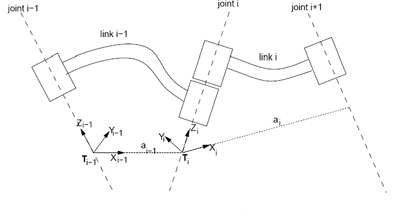
In order to easily locate each link, we define a corresponding coordinate frame: frame i is attached to the link i. Denavit and Hartenberg proposed a matrix method to assign systematically coordinate systems to each link in an articulated chain.

The link and joint parameters may be summarized as:

• link twist α: the angle from the Zi-1 axis to the Zi axis about the Xi-1 axis;
• link length a: the offset distance between the Zi-1 and Zi axes along the Xi-1 axis;
• joint angle θ: the angle between the Xi-1 and Xi axes about the Zi axis.
• link offset d: the distance from the origin of frame Xi-1 to the Xi axis along the Zi axis;

Joint Name	α (radians)	a (meters)	θ (radians)	d (meters)
HeadYaw	0.0	0.0	0.0	0.0
HeadPitch	-PI/2	0.0	-PI/2	0.0
LShoulderPitch	-PI/2	0.0	0.0	0.0
LShoulderRoll	PI/2	0.0	PI/2	0.0
LElbowYaw	PI/2	0.0	0.0	UpperArmLength
LElbowRoll	-PI/2	0.0	0.0	0.0
LWristYaw	PI/2	0.0	0.0	LowerArmLength
LHipYawPitch	-3/4 * PI	0.0	-PI/2	0.0
LHipRoll	-PI/2	0.0	PI/4	0.0
LHipPitch	PI/2	0.0	0.0	0.0
LKneePitch	0.0	-ThighLength	0.0	0.0
LAnklePitch	0.0	-TibiaLength	0.0	0.0
LAnkleRoll	-PI/2	0.0	0.0	0.0
RHipYawPitch	-PI/4	0.0	-PI/2	0.0
RHipRoll	-PI/2	0.0	-PI/4	0.0
RHipPitch	PI/2	0.0	0.0	0.0
RKneePitch	0.0	-ThighLength	0.0	0.0
RAnklePitch	0.0	-TibiaLength	0.0	0.0
RAnkleRoll	-PI/2	0.0	0.0	0.0
RShoulderPitch	-PI/2	0.0	0.0	0.0
RShoulderRoll	PI/2	0.0	PI/2	0.0
RElbowYaw	PI/2	0.0	0.0	UpperArmLength
RElbowRoll	-PI/2	0.0	0.0	0.0
RWristYaw	PI/2	0.0	0.0	LowerArmLength

Base Transforms

The transforms below are used to move from the torso reference to the first joint in the chain.

Chain	Base Transform
Head	Translation( 0, 0, NeckOffsetZ )
LArm	Translation( 0, ShoulderOffsetY, ShoulderOffsetZ )
LLeg	Translation( 0, HipOffsetY, -HipOffsetZ )
RLeg	Translation( 0, -HipOffsetY, -HipOffsetZ )
RArm	Translation( 0, -ShoulderOffsetY, ShoulderOffsetZ )

End Transforms

To move from the last joint in the chain to an interesting point to control in the same initial rotation as the torso, end transforms are used.

Chain	End Transform
Head	RotX( Pi/2 ).RotY( Pi/2 )
LArm	RotX( -Pi/2 ).RotZ( -Pi/2 ).Translation( HandOffsetX, 0, -HandOffsetZ )
LLeg	RotZ( Pi ).RotY( -Pi/2 ).Translation( 0, 0, -FootHeight )
RLeg	RotZ( Pi ).RotY( -Pi/2 ).Translation( 0, 0, -FootHeight )
RArm	RotX( -Pi/2 ).RotZ( -Pi/2 ).Translation( HandOffsetX, 0, -HandOffsetZ )

Please see the hardware documentation for the definitions of these constants.

<< Previous

Next >>